
The population mean μ is related to a specified The table below shows three sets of hypotheses. True, the other must be false and vice versa. The hypotheses are stated in suchĪ way that they are mutually exclusive. (2) formulate an analysis plan, (3) analyze sample data, andĮvery hypothesis test requires the analystĪlternative hypothesis. This approach consists of four steps: (1) state the hypotheses,
Two tailed hypothesis test calculator using p value how to#
This lesson explains how to conduct a hypothesis test of a mean, AP stat formulas Hypothesis Test for a Mean.Confidence interval Confidence intervals.Simulation of events Discrete variables.Diff between means Statistical InferenceĪP Statistics: Table of Contents The basics.Experimental design Anticipating Patterns.P-value (0.153) > Significance level (0.We fail to reject the null hypothesis considering the following: The sample returns a mean of 56 with a standard deviation of 28: The company takes a sample of 100 boxes to test if there should be support for the null hypothesis that the mean value is 60 units. The boxes are accepted for shipping if they have a maximum of 63 and a minimum of 57 cookies. Say a production line must pack 60 Danish butter cookies per box. Take the following example of quality assurance in a production line:
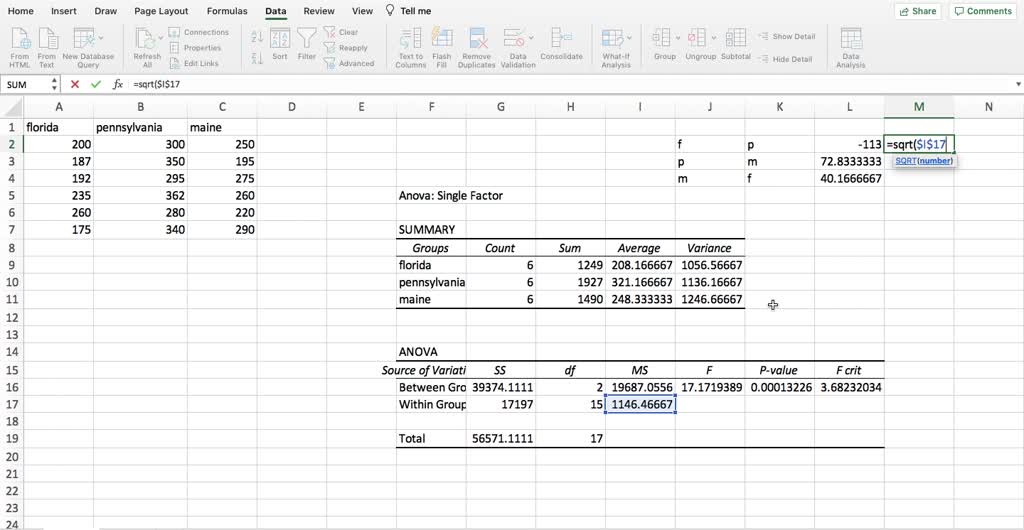
The functions =STANDARDIZE =NORM.S.INV and =NORM.S.DIST can be used to support a hypothesis testing in Excel. The p-value of 0.089 tells us that there is approximately 8.9% probability of getting a result at least as extreme as ours assuming that the mean is 6.58.

Therefore, based on our sample, we do not find evidence that the assumed mean should be different from 6.58.
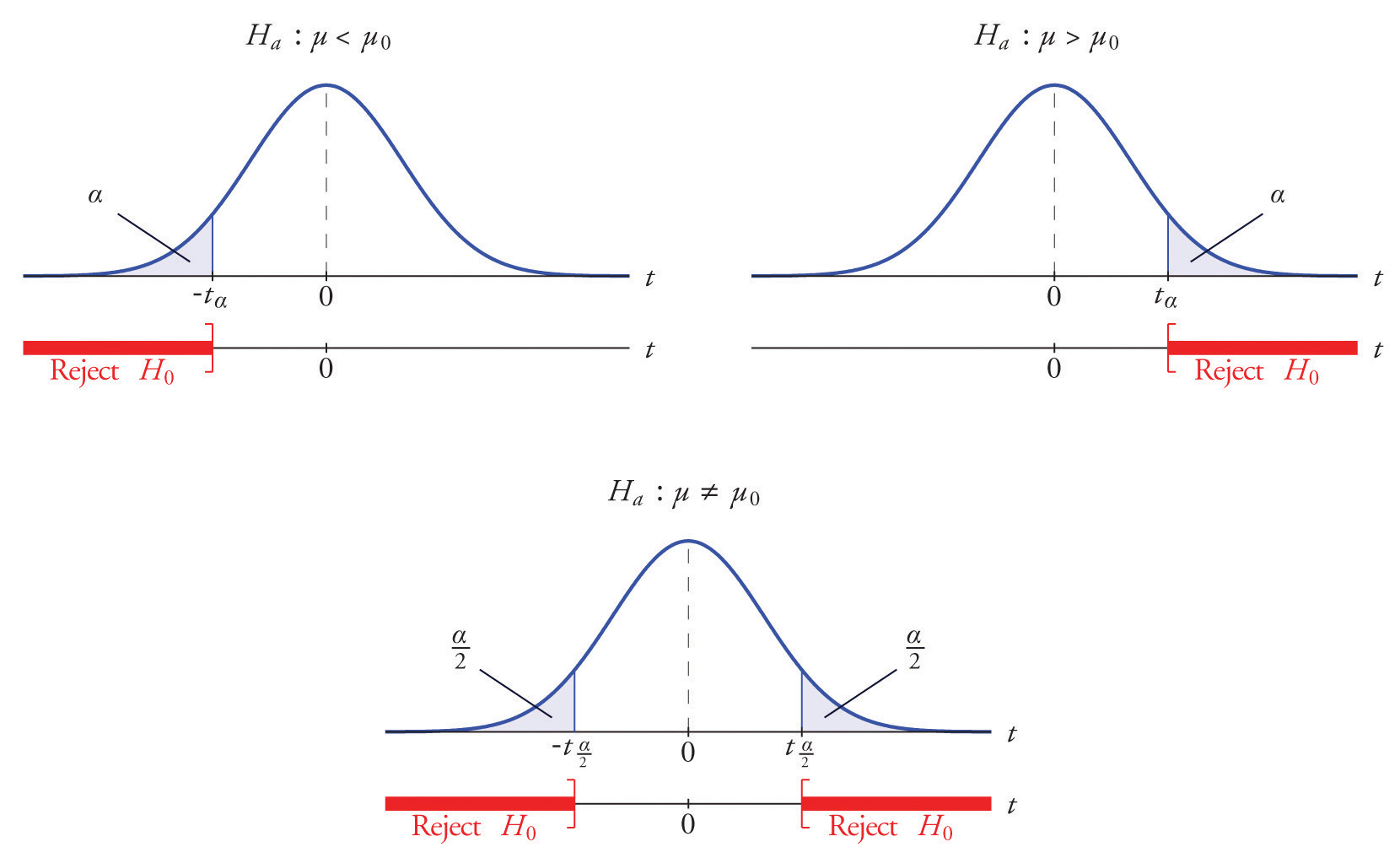
The z-score falls in non-rejection area, so we fail to reject the null hypothesis. Looking up in the z-table, a z-score of -1.698 returns a p-value of 0.089. The z-score of -1.698 is within the acceptance area as it is does not go below the critical value of -1.96, nor above the 1.96. Our n = 100, so our test statistic will be applied with the normal standard table: The Central Limit Theorem says that the greater the sample size the more any probability distribution approximates to the normal distribution and it is usual to see the this applied for n>30. Now, the company takes a simple random sample of 100 balls and the results are: The production will be put on hold at a statistical significance greater than 5%, so the significance level (α) = 0.05 HA: µ ≠ 6.58 Step 2: Setting significance level The hypotheses and significance level are specified. The procedure for conducting the two-tailed test is the same as for one-tailed tests and following the general procedure for hypothesis testing. A simple random sample of 100 balls is planned to be taken and, in the case, that the production has a statistical significance greater than 5%, production will be put on hold and the production line adjusted. Say that a production line of tennis balls supplying The International Tennis Federation must produce and deliver all balls with a diameter of 6.58 cm. The critical values are set at the α/2 level and determine the upper and lower limits of the rejection areas:Īs opposed to the one-tailed test, the two-tailed test splits the significance level into both tail which leads to a significantly different basis for the statistical inference: If the value tested for falls beyond the upper limit or lower limit, the null hypothesis is rejected, and it is then inferenced as “statistically significant”. Testing if it is ‘ different from’ implies to test if it is “significantly” greater than or “significantly” less than µ. The two-tailed test is applied to test if a certain value is “significantly” different from µ.

It can typically be a new finding that is tested to see if it is “significantly” different from the assumed mean (µ). Hypothesis testing is applied to calculate the statistical significance of a claim. a 5% alpha level leaves divided into 2.5% in each tail.


 0 kommentar(er)
0 kommentar(er)
